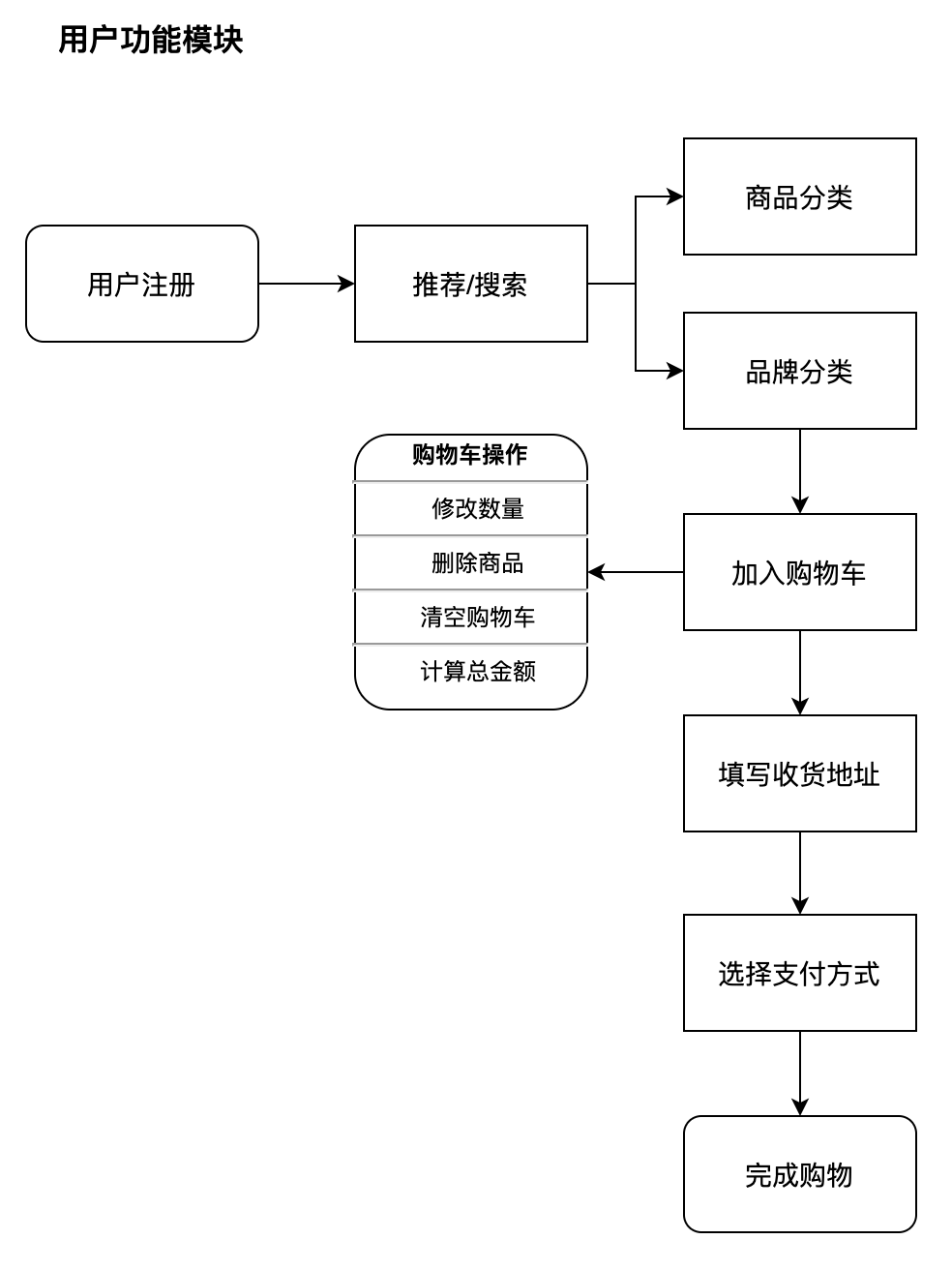
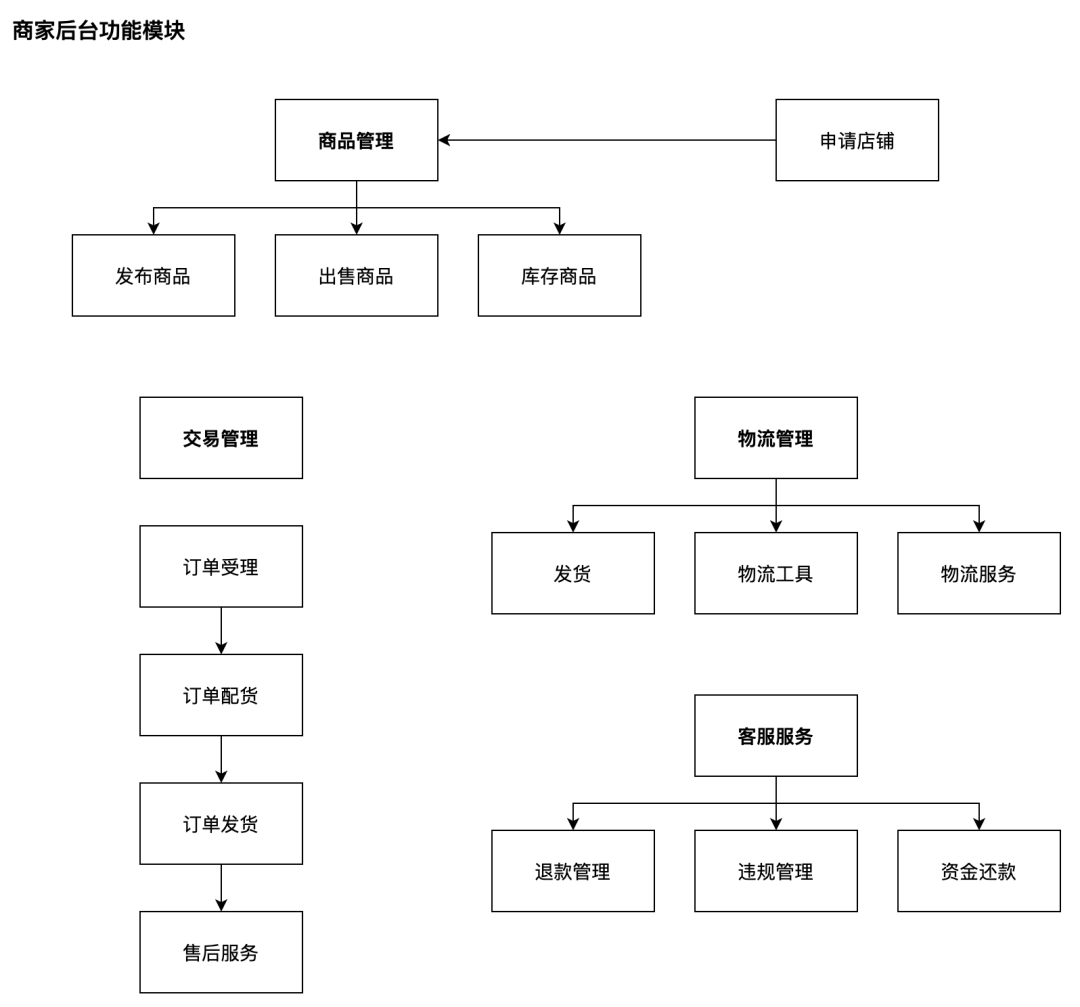
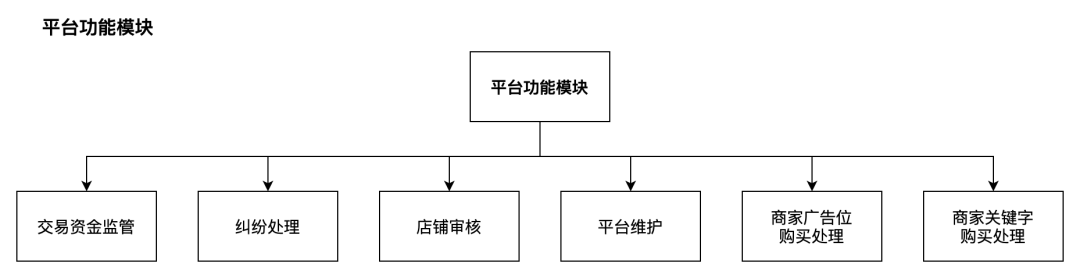
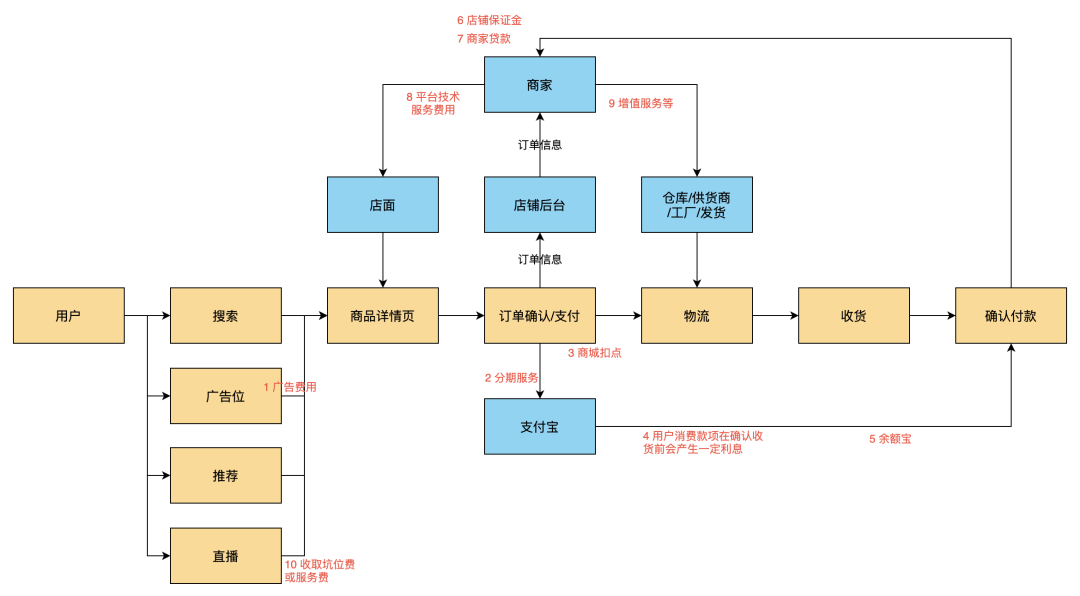
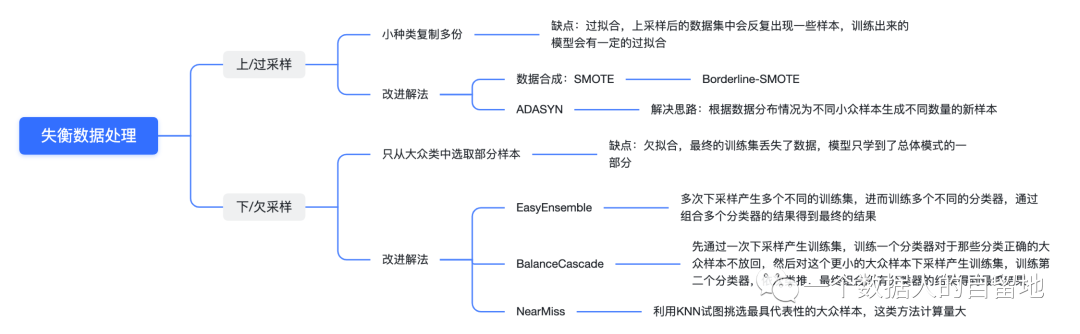
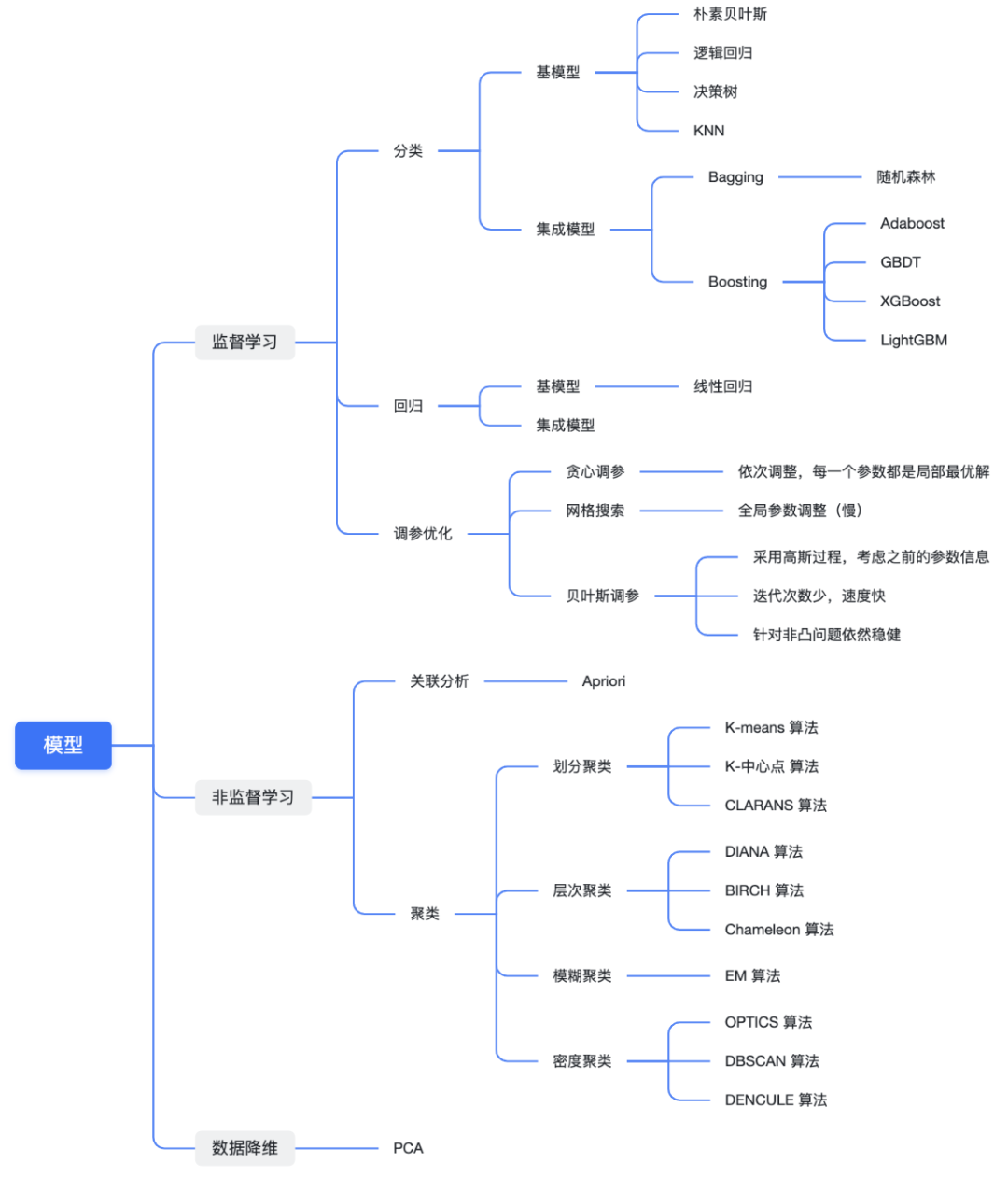
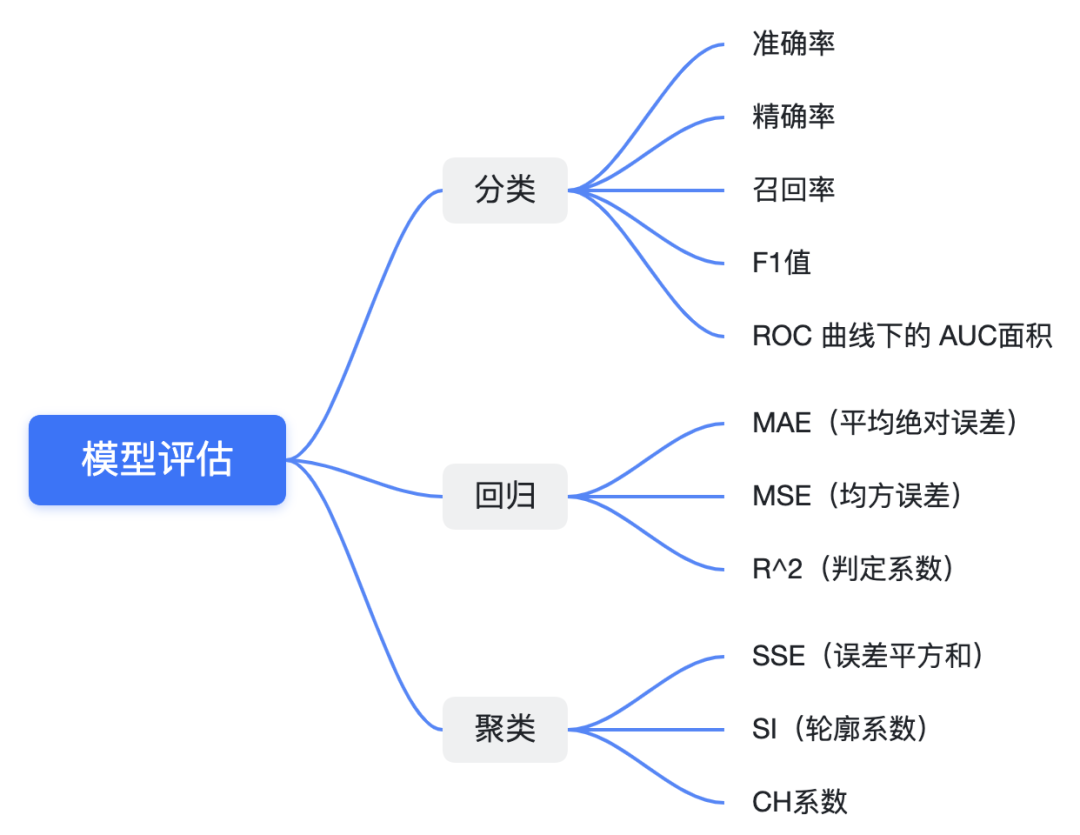
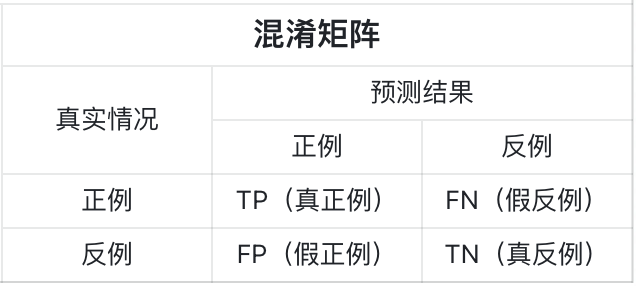
关注公众号,回复“进群”,与3万+数据人交流 作者介绍 @猫耳朵 数据产品经理萌新, 开发经验丰富,专注于数据产品; “数据人创作者联盟”成员。 01 电商B2C模式介绍 做电商商城已经成为热门行业,传统电子商务的几种商业模式分别为B2B、B2C、C2C、C2B、O2O等。今天我们着重研究一下B2C模式。 B2C模式,是指进行电子商务交易的供方是商家(或企业、公司),买方是个人消费者,他们利用互联网技术和电子商务平台完成交易。随着我国电子商务不断的发展,B2C模式也衍生了不同类型的商业模式,具体可分为四类,如下表: 其中,京东、天猫的盈利方式:特许加盟、虚拟店铺出租费、广告费、技术服务费等。 1.1 B2C主要业务功能 1.2 平台的盈利模式 02 数据挖掘流程 2.1 商业理解 商业理解(Business understanding)该阶段是数据挖掘中最重要的一个部分,在这个阶段里需要明确商业目标、评估商业环境、确定挖掘目标以及产生一个项目计划。 2.2 数据理解 数据理解(Data understanding):在数据理解过程中我们要知道都有些什么数据,这些数据的特征是什么,可以通过对数据的描述性分析得到数据的特征。 了解数据集基本特征 info; 查看数据分布情况 describe; 查看缺失值及占比,对缺失值过多(大于80%)的数据进行删除。 2.3 数据准备 数据准备(Data preparation):在该阶段我们需要对数据作出提取、清洗、合并、标准化等工作。选出要进行分析的数据,并对不符合模型输入要求的数据进行标准化操作。 缺失值处理的几点建议: 小于20%采取方案补充; 20%~50%之间采取多值离散化; 50%~80%之间采取二值离散化; 大于80%的删除。 不平衡数据处理 所谓的不平衡数据集指的是数据集各个类别的样本量极不均衡。以二分类问题为例,假设正类的样本数量远大于负类的样本数量,通常情况下把多数类样本的比例接近100:1的数据称为不平衡数据。 不平衡数据的场景出现在互联网应用的方方面面,如搜索引擎的点击预测(点击的网页往往占据很小的比例),电子商务领域的商品推荐(推荐的商品被购买的比例很低),信用卡欺诈检测,网络攻击识别等等。 常用的处理方式如下: 2.4 建立模型 建立模型(Modeling):需要根据分析目标选出适合的模型工具,通过样本建立模型并对模型进行评估。 2.5 模型评估 模型评估(Evaluation):一方面利用挖掘工具自带评估模型进行挖掘模型效果评估,如准确率、精确度等;另一方面,抽样一部分结果进行调研验证分析。 模型评估的意义 在完成模型构建之后,必须对模型的效果进行评估,根据评估效果来继续调整模型的参数、特征或者算法,以达到满意的结果。 评价一个模型最简单也是最常用的指标就是准确率,但是在没有任何前提下使用准确率作为评价指标,准确率往往不能反映一个模型性能的好坏,例如在不平衡的数据集上,正类样本占总数的95%,负类样本占总数的5%。那么有一个模型把所有样本全部判断为正类,该模型也能达到95%的准确率,但是这个模型没有任何的意义。 因此,对于一个模型,我们需要从不同的方面去判断它的性能。在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评价结果。 这意味着模型的好坏是相对的,什么样的模型是好的,不仅取决于算法和数据,还决定于任务需求。例如医院中监测病人是否有心脏病的模型,那么这个模型的目标是将所有有病的人给监测出来,即使会有许多误诊(将没有病监测为有病)。 再例如,在警察追捕罪犯的模型上,该模型的目标是将罪犯准确的识别出来,而不希望有过多的误判(将正常人认为是罪犯)。所以不同的任务需求,模型的训练目标不同,因此评价模型性能的指标也会有差异。 根据模型选择其模型评估方式 2.5.1 分类算法评估 下面以二分类为例,对分类模型中的常用指标进行说明与总结。 混淆矩阵(Confusion Matrix) 真正(True Positive,TP):实际为正预测为正; 假正(False Positive,FP):实际为负但预测为正; 假负(False Negative,FN):实际为正但预测为负; 真反(True Negative,TN):实际为负预测为负。 1. 准确率(Accuracy) 2. 精确率(Precision) 3. 召回率(Recall) 4. F值 5. ROC曲线和AUC AUC(Area Under the ROC Curve)指标是在二分类问题中,模型评估阶段常用作最重要的评估指标来衡量模型的稳定性。 根据混淆矩阵,还可以得到另外两个指标: 真正率(True Positive Rate,TPR):即被预测为正的正样本数/正样本实际数。 假正率(False Positive Rate,FPR):即被预测为正的负样本数/负样本实际数。 ROC曲线,Y轴TPR,X轴FPR,作图,便得到了ROC曲线,而AUC则是ROC曲线下的面积。 AUC=1 最理想;0.7~0.9准确率比较高;0.5无诊断价值。 概率,默认阈值0.5。 ROC曲线作用:1. 确定阈值,2. 得到AUC面积。 2.5.2 回归算法评估 按照数据集的目标值选择模型,目标值为连续型的需要采用回归模型。 1. 平均绝对误差 平均绝对误差(Mean Absolute Error,MAE):又被称为L1范数损失。MAE是基于误差的绝对值,而非平方差,因此相比较于MSE与RMSE来说更直观地体现出预测值和实际值的差距。 Python Sklearn : 2. 均方误差 均方误差(Mean Squared Error,MSE),观测值与真值偏差的平方和与观测次数的比值。 Python Skearn: 这也是线性回归中最常用的损失函数,线性回归过程中尽量让该损失函数最小。那么模型之间的对比也可以用它来比较。 MSE可以评估数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。 MSE可以衍生得到均方根方差(Root Mean Square Error,RMSE),和本身的目标值有关系,不同数据源不能对比模型的优劣。 3. R^2判定系数 Python Sklearn: 数学理解:分母理解为原始数据的离散程度,分子为预测数据和原始数据的误差,二者相除可以消除原始数据离散程度的影响。其实,R^2判定系数是通过数据的变化表征一个拟合的好坏。 正常取值范围为[0,1]——实际操作中通常会选择拟合较好的曲线计算R^2。越接近1,表明方程的变量对目标值的解释能力越强,这个模型对数据拟合的也较好;越接近0,表明模型拟合的越差。经验值:>0.4,拟合效果好。 数据集的样本越大,R^2越大,因此,不同数据集的模型结果比较会有一定的误差。 2.5.3 聚类算法评估 1. 误差平方和 误差平方和(Sum of Square Error,SSE),刻画的簇内的凝聚程度。 肘点法则:下降率突然变缓时即认为是最佳的k值(随着簇数越多,SSE越小)。 2. 轮廓系数 轮廓系数(Silhouette Coefficient,SI)是聚类效果好坏的一种评价方式。最早由Peter J. Rousseeuw 在1986年提出。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。 方法: 1)计算样本i到同簇其他样本的平均距离ai。ai越小,说明样本i越应该被聚类到该簇。将ai称为样本i的簇内不相似度。簇C中所有样本的ai均值称为簇C的簇不相似度。 2)计算样本i到其他某簇Cj的所有样本的平均距离bij,称为样本i与簇Cj的不相似度。定义为样本i的簇间不相似度:bi=min{bi1, bi2, ……, bik},bi越大,说明样本i越不属于其他簇。 3)根据样本i的簇内不相似度ai和簇间不相似度bi,定义样本i的轮廓系数。 那么i向量轮廓系数就为: a(i):i向量到同一簇内其他点不相似程度的平均值。 b(i):i向量到其他簇的平均不相似程度的最小值。 判断: 1)轮廓系数范围在[-1, 1]之间。该值越大,越合理。SI接近1,则说明样本i聚类合理;SI接近-1,则说明样本i更应该分类到另外的簇。 2)若SI近似为0,则说明样本i在两个簇的边界上。 3)所有样本的SI的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。 将所有点的轮廓系数求平均,就是该聚类结果总的轮廓系数。 3. CH系数 CH系数(Calinski-Harabasz Index):类别内部数据的协方差越小越好,类别之间的协方差越大越好。这样Calinski-Harabasz分数s会高,分数s高则聚类效果越好。 tr为矩阵的迹,Bk为类别之间的协方差矩阵,Wk为类别内部数据的协方差矩阵。 m为训练集样本数,k为类别数。 使用矩阵的迹进行求解的理解:矩阵的对角线可以表示一个物体的相似性。 在机器学习里,主要为了获取数据的特征值,那么就是说,在任何一个矩阵计算出来之后,都可以简单化,只要获取矩阵的迹,就可以表示这一块数据的最重要的特征了,这样就可以把很多无关紧要的数据删除掉,达到简化数据,提高处理速度。 CH需要达到的目的:用尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果。 2.6 部署 部署(Deployment):得出模型的挖掘结果不是最终目标,还需要考虑,如何更直观可视化的进行结果展示,如何提升数据挖掘结果对实际业务的支撑能力。随着业务不断发展,模型也需要随之调整和优化,在不断的使用和优化中持续发展。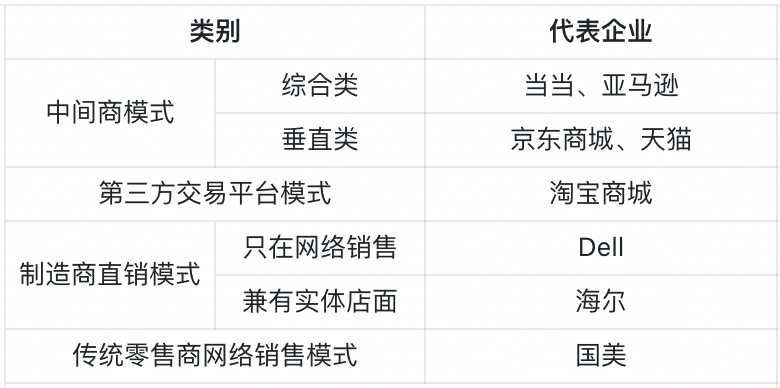


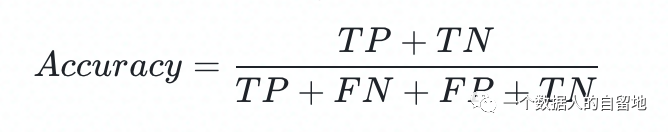
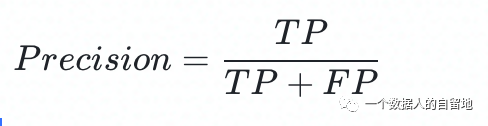


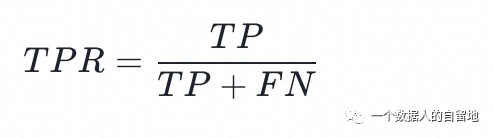
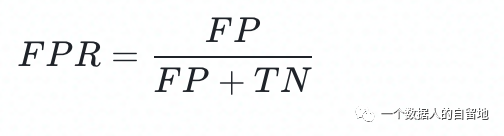

print("MAE:", metrics.mean_absolute_error(y_test, pred))
from sklearn import metricsprint("MSE:", metrics.mean_squared_error(y_test, pred))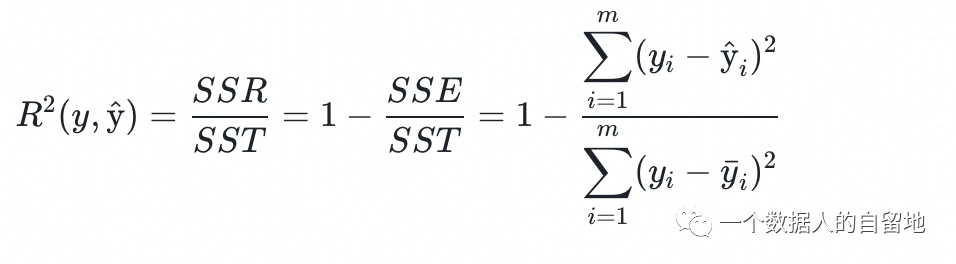
print('R^2 score:', metrics.r2_score(y_test, pred, sample_weight=None, multioutput='uniform_average'))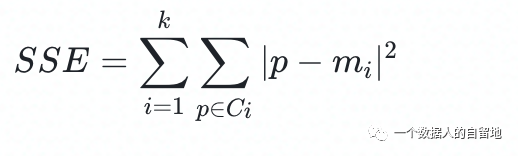
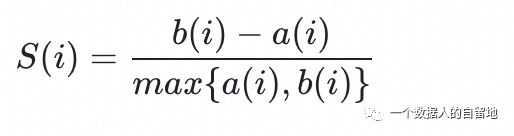
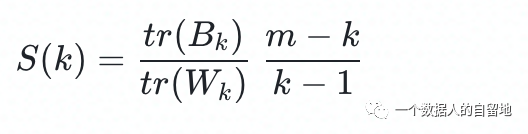
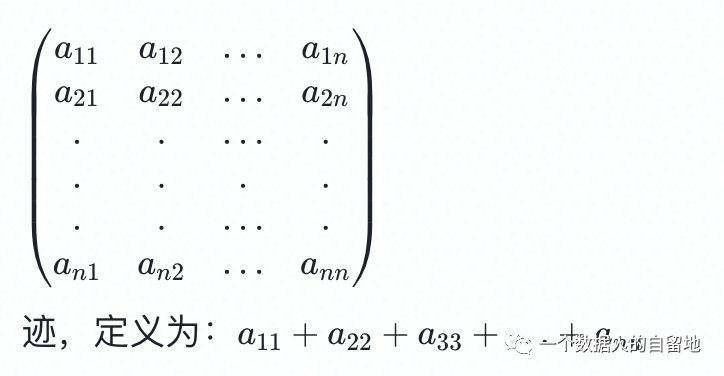
投稿

微信公众账号
微信扫一扫加关注
评论 返回
顶部


发表评论 取消回复